本篇文章对链路预测中的3个准局部相似性指标做阐述。

准局部相似性指标考虑的信息比局部指标更多，而放弃对预测精度没有贡献或贡献很小的多余信息。

（1）\small Local\ Path\ Index (LP)。其作用范围比\small CN更广，定义为：

S^{LP}=A^2+\epsilon A^3，

\small \epsilon是自由参数。显然，当\small \epsilon=0时，这个度量退化为\small CN。如果\small x和\small y不是直接连接的，\small A^3_{xy}等于连接x和y的长度为3的不同路径的数目，有：

S^{LP(n)}=A^2+\epsilon A^3+\epsilon^2 A^4+...+\epsilon^{n-2}A^n，

2">\small n>2为最大阶数。随着\small n的增加，这一指标对信息量和计算量提出了更高的要求。特别地，当\small n→∞时，\small S^{LP}_N将等价于考虑网络中所有路径的\small katz指数。该指标在不相关网络中的计算复杂度为\small O(N(k)^n)，随\small n的增加而迅速增长，当\small n较大时，将超过\small Katz指标的计算复杂度(近似于\small O(N^3))。实验结果表明，最优\small n与网络的平均最短距离呈正相关。

\small LP指标的性能明显优于基于邻域的索引，如\small RA、AA、CN。这是因为邻域信息的可区分性较差，并且两个节点对被分配相同的相似度分数的概率很高。以INT网络为例，其共有\small 107多个节点对，其中\small 99.59\%的节点对被\small CN赋值为零。对于得分高于\small 0的所有节点对，\small 91.11\%被分配得分\small 1，\small 4.48\%被分配得分\small 2。使用更多涉及下一个最近邻居的信息可能会打破状态的退化，并使相似性得分更容易区分。这就是\small LP指标大幅提高预测精度的原因。

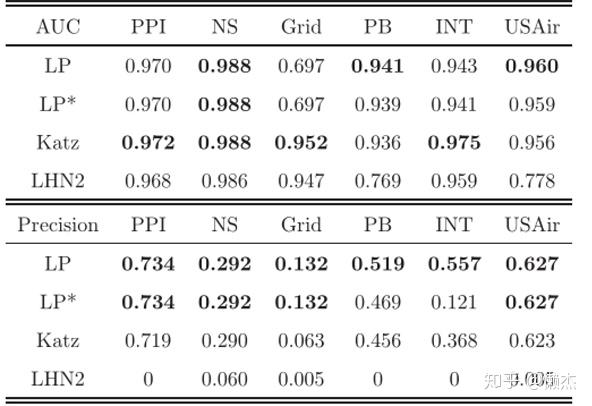
\small LP指标与另外两个依赖路径的全局指标(\small Katz和\small LHN2指标)的比较如图所示，根据\small AUC值，\small Katz指标执行得最好，而\small LP指标对于\small Precision而言是最好的。对于平均最短距离较小的网络(例如，USAIR和PB)，\small LP指标对\small AUC和\small Precision给出了最准确的预测。总而言之，与全局指标相比，而\small LP指标提供了具有竞争力的良好预测，同时计算量要少得多。

（2）Local\ Random\ Walk\ (LRW)。为了测量节点\small x和\small y之间的相似性，首先在节点\small x上放置一个随机游走器，因此初始密度向量\small \vec \pi_x (0) = \vec e_x。当\small t≥0时，该密度向量演化为\small \vec \pi_x (t+1) = P^T \vec \pi_x (t)，则\small LRW指标在时间步长\small t定义为：

S^{LRW}_{xy} = q_x \pi_{xy} (t) +q_y \pi_{yx} (t)

其中\small q是初始配置函数。在文献Link Prediction based on Local Random Walk中\small Liu和\small Lü应用了一个由节点度决定的简单形式，即\small q_x =\frac {k_x}{M}。

（3） Superposed\ Random\ Walk\ (SRW)。与\small LRW类似，在起始点连续释放随机游走者，使得目标节点与附近节点具有更高的相似度。数学表达式为

\small s^{SRW}_{xy} = \sum^{t}_{\tau =1} s_{xy}^{LRW}(\tau) = \sum^{t}_{\tau =1} [q_x \pi_{xy}(\tau) + q_y \pi_{yx}(\tau)]

\small t为时间步长。

将指标\small LRW和\small SRW与三个局部(或准局部)指标\small CN、RA、LP，以及另外两个基于随机游走的全局指数\small ACT、RWR和层次结构方法\small (HSM)进行比较。结果如图：

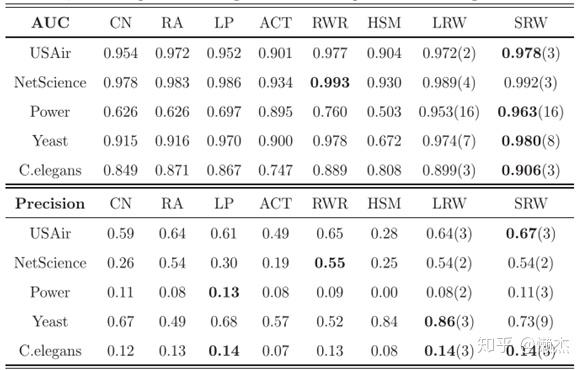
\small LP的参数\small ε=10^{−3}(在\small USAIR为\small ε=−10^{−3})，\small RWR的参数\small c=0.9。括号内的数字表示LRW和SRW标数的最佳步长。例如，\small 0.972(2)表示在\small LRW的第二步获得最佳\small AUC值。

\small LRW和\small SRW方法的性能优于其他指标，它们各自的最优步行步长与网络的平均最短距离呈正相关。此外，\small LRW和\small SRW的计算复杂度低于\small ACT和\small RWR，其求逆和伪逆的时间复杂度约为\small O(N^3)，而\small n步\small LRW和\small SRW的时间复杂度约为\small O(N(k)^n)，忽略了网络的异构度。也就是说，当\small n较小时，\small LRW和\small SRW的运行速度远远快于其他基于随机游走的全局相似性指数。\small LRW和\small SRW具有计算复杂度低的优点，在大型(即大\small N)和稀疏(即小\small (K))网络中尤为突出。\small SRW与\small LRW和\small SRW动机相似。\small SRW应用于解决分类问题，既能降低时间复杂度，又能降低空间复杂度。