谢邀！关于如何学习高中理科，下文我将以高中数学为例，说明理科的学习方法。

在我接触了越来越多学生后，发现几乎所有学不好理科的孩子都存在以下问题。以数学为例，如果把基础问题解决，高考数学是能拿到120的，其后就是数学思维问题：

1. 基础（定义，定理）不扎实

我当年学数学的时候，没有这个毛病。但随着我接触的孩子越来越多，我发现很多孩子很努力，但是根本不会学习，尤其是不会仔细体会和品味这些理科的概念。他们很努力，拼命刷题，但仍然对这些概念一知半解。甚至还有同学质疑，说“不用掌握概念我也可以做题”。是的，你的确可以做一部分题，但题目一变，你就完蛋。

很多同学这题做不出来。我结合数学三招来解答：

首先，解决数学问题，我们不喜欢中文，要“翻译”为数学语言，例如画张图（几何语言）

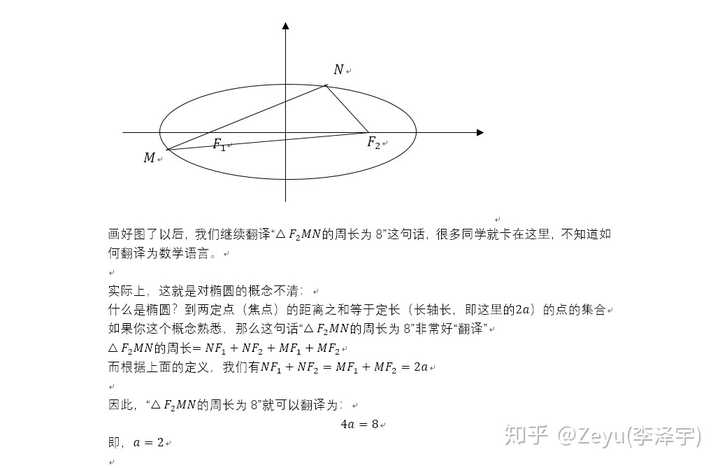
因此这道题的第一问一点都不难，如果你对于椭圆的定义不熟悉，你即使会数学思维“翻译”，知道要把中文翻译为数学语言，你也无从下手！

请记住：如果说数学思维就像是成为米其林三星大厨需要具备的手艺的话，那么基础知识就是备菜。巧妇难为无米之炊，如果你的米没有洗好，肉没有切好，锅没有洗干净，你的技艺再高超，也不可能做好一道菜。

那基础概念应该如何学习呢？

（1） 精读

其实数学也好，科学（物理，化学等）也罢和诗歌是非常相似的，都是在试图用最精炼的语言表达：数学/科学是刻画我们所处的外在环境-大自然的万千现象，诗歌是刻画我们的内心复杂的感情。

因此这样的东西是没有一个字是多余的。一定要精读，一个词一个词的理解，不要像小说一样的去泛读。

例如，我们刚刚讲了什么叫做椭圆，那你别急着看下文，思考一下什么叫做双曲线？

很多人的回答是：“到两定点的距离之差等于定长的点的集合”，很遗憾这是错的。

正确的答案是：“到两定点的距离之差的绝对值等于定长的点的集合（两定点线段长>这个绝对值>0）”，没有了“绝对值”三个字，得出来的是双曲线的一个分支。

如果我是高考命题人，我可以轻松出一道题目，就考这个基本概念，我估计又会“死掉”一大片。

学习物理又何尝不是如此？例如什么叫摩擦力？

同学们要学会精读，并且理解这些定义和概念。你们高中课本的定义是这样写的：

阻碍物体相对运动（或相对运动趋势）的力叫做摩擦力。

我们来一点一点的理解：

一个力是向量，因此你必须说清楚其大小和方向

首先是方向，摩擦力既然是”阻碍”，因此其方向是和相对运动方向相反的，也就是说和速度(以接触的物体作为参照物）方向相反！那么什么叫做相对运动趋势？即，假如没有摩擦力，这个物体会如何动（以接触的物体作为参照物）？摩擦力的方向就和这个运动方向相反。

例如一个往前移动的传送带上的物体（物体跟着传送带运动），为什么摩擦力方向是向前的？

这里就要求你对“相对运动趋势”理解深刻。如果没有摩擦力（绝对光滑），传送带上的物体将保持静止。那么相对于传送带（以传送带作为参照物），其运动方向是向后的，这就是相对运动方向。因此摩擦力应该和这个方向相反。

那么大小呢？分为静摩擦和动摩擦两种，静摩擦用受力平衡来确定，而动摩擦力的大小= \mu N

这样不就十分清楚了？以后遇到任何关于摩擦力的问题，你都可以轻松的利用上面的定义“翻译”为物理中力的语言（物理模型），而后翻译为数学语言，解之，即可。

（2） 费曼学习法

现阶段，不要求大家使用类比等思维方式深层次地理解每一个概念背后的逻辑，然后表达得连一个小学生也听得懂。

你只需要这样做：

用自己的话，在一分钟内把这个概念或者定理复述一遍。然后利用微信录音，QQ录音等录下来，之后对比你讲的和教科书上的内容。如果一致，那么就说明你懂了，如果不一致，或者说不清楚，说不出来，那么不好意思，你这个概念掌握得比较差。

我非常相信王阳明先生的“知行合一”四个字，知而不行就是未知。在你运用这些概念之前，最起码的“行”就是能够说得出来，连说都说不出来，谈什么知呢？

这也是用来自我检验基础概念的极佳方法。

例如你自己问自己，高中阶段证明线面垂直至少可以有5个不同的定理，你能很快把他们说出来吗？如果不能，你就知道你的立体几何的基础不够扎实。

（3）所有说不用复习基础就可以提分的都是骗子

有一部分不负责任的人，为了赚钱，弄出一堆什么“模板”“秒杀”，并宣称“不用复习基础就会做题”。听起来特别牛，其实害人不浅。

首先，从逻辑上来说，你的思维方式再高明，你可能在两个小时内倒推数学家几百年确定的各种定义和定理吗？

再者，这类模板秒杀我们金融上叫做“curve fitting”。他的模板只适合他精心挑选的一小类题目，题目一改，就阵亡。在高考题越来越灵活的今天，靠这些垃圾，考试如何能够提高？未来更是误人终生！

记住：天上不会掉馅饼，如果掉了，注意是骗局。

2. 不掐着时间做题

考试，无论你喜欢还是不喜欢，最大的特点就是有时间限制。因此，一个能拿高分的人一定是简单的题目做得又快又对，这样他/她才有时间思考难题。

因此，平常练习就应该掐着时间做。例如选择填空题就尽量不要超5分钟。如果超过了，就把它当做是错题 – 运用数学三招思考，还有更加简单的方法吗 （例如特殊化）？我能总结什么模式？我需要记忆什么快速解答的公式吗？

另外这样练习也让你十分熟悉考试的压力和紧张感。真正考试的时候就不容易发挥失常。

3. 不会从错误中学习

我先定义以下什么是错题：

1. 做错的题（包括3中：粗心，概念不清，以及逻辑问题，这三者一定要严格区分开来）

2. 不会做的题

3. 做得慢，没有在规定时间做完的题

都是你的错题。

很多同学遇到错题，就扫一遍答案，看懂了，然后？然后就没有然后了。

这样的学习，恕我直言，你是在浪费题目和时间！这样日积月累，你表面上很努力，不过只是在重复做无用功罢了。

记住：错误是一个人最大的学习之源！

我的一生最重要的原则，方法都是从错误（自己的+别人的）中学来的。正如孟子所言，闻过而喜。（我现在还没有达到他的程度，出现问题我往往还是比较不爽的，达不到“喜”的程度）

那么如何从错误中学习呢？我总结了以下反馈环

遇到错误，首先的就是要找原因。

例如，我的答案错了，是为什么？粗心，概念不清，还是逻辑不清？

例如有的同学在变换： (x^2-1)/(x-1)

直接写：

(x^2-1)/(x-1)=x+1

这不是粗心，而是逻辑不清。你没有意识到你的变换不是充要变换，因为你舍去了一个限制条件（ x\neq1 ），因此会出现增根。

扩而广之，你要知道，天下间所有的题目只有两类，判断题（包括证明题）和求解题。而求解题是求满足某个条件的某未知数的取值范围。必须是这个条件的充要变化才无增根，无失根，是完美的解。如果你转化为其必要条件，例如上面的变化，那就记得要检验。

这样，你对这个错误才真正学到东西了！

那么做不出来，做得慢呢？记住，看懂答案为什么是对的远远不够，关键是你要弄清楚下一次你要如何想，才能把这道题又快又对地做出来 – 即解题思维是什么

这个思维就是我提到的数学哲学和数学三招。 有的同学学了，还是解不出题目，你就要思考，是不是我对数学三招的理解不够？首先我能用自己的话把数学三招说出来吗？我有什么技巧没有掌握？

我用下面的例子具体来说明吧：

很多同学做不出这道题。注意，做不出来也是错题！

然后他们去看答案，答案看懂了，就没有然后了。这对你解题有意义吗？一点意义也没有。

关键是未来如何思考才能解决这样的问题，思路在哪里。

这题背后的思路就是我们的第二招，特殊化。

原则：证伪比证明容易得多（因为只需要找到一个反例即可），因此对于选择题，很多时候我们可以用特殊的例子证伪三个选项，虽然我们没有证明最后的选项是正确的，但只要这道题不是错题，我们就可以选择了。这是特殊化的一个运用。

对于这题来说，我希望找到符合前面绝对值不等式的 a,b,c 但和后面 a^2+b^2+c^2＜100矛盾的特殊值，怎么办？

首先，要和后面矛盾，一个临界值就是10，因为若a,b,c 中其中有一个是10，后面的不等式就错了。这个就是我们的入手点。（技巧：特殊化的时候优先从极端，特殊的开始）

对于A,代入 a=10 ，发现 b 和其是对称的，因此我们也取 b=10 （这又是一个技巧，对称时候我们往往可以从相等的数开始，因为极端，特殊），然后取 c=-110 就成功找到反例了。

对于B，代入 a=10 ，为了使得绝对值中很小，取 b=-100, c=0 即可，又找到反例了

对于C，取 a=10, b=-10, c=0 即可推翻

因此答案是D，我们无需在D上面浪费哪怕一秒钟。

从这道题你就学会了特殊化思维中的很多技巧。这样，每一题对你来说都有所得，然后你再在下一题中检验你的所得，很快，你的水平不就直线上升了？

关于错误，我还有很多推论，例如：领导力中的：一个不允许员工犯错的领导不是好领导，一个不允许孩子犯错的家长不是好家长

创业中：很多时候，犯错在所难免，我们要加速犯错的过程，犯小错，学大道理

这些不是这篇文章的内容，有机会再写一个文章细说。

我想同学们通过我的这篇文章应该学会如何学习。这篇文章的道理也适用于物理，化学，GMAT等的学习。希望大家数学进步！