微信号 ：supermodeling

原文标题：斐波那契数列趣谈

via 善科

by BB

一般认为斐波那契数列的提出是基于兔子的繁殖问题：如果一开始有一对兔子，它们每月生育一对兔子，小兔在出生后一个月又开始生育且繁殖情况与最初的那对兔子一样，那么一年后有多少对兔子？

答案是，每月兔子的总数可以用以下数列表示：1，1，2，3，5，8，13，21，34，55，89，144，233…。

这一数列是意大利数论家列奥纳多·斐波那契（Leonardo Fibonacci）在他13世纪初的著作Liber Abaci中最早提出的。如果取数列前两个元素为1，那么递推关系就是：

当然，曾经有一度数学家们将0作为斐波那契数列的首项（或第0项）。

这一数列看起来相当简单，但却隐藏着一些有趣的东西。

关于数列元素

关于斐波那契数列的元素，人们发现了不少有意思的事情。

质数与合数：斐波那契数列的质数元素也是该数列的质数项，唯一的例外是第4项元素3。但这个规律反过来不成立，数列的质数项元素的也可能是合数。这一“规律”可以为人们提供搜索大质数的线索。但在相当大的元素以后是不是仍有这个规律呢？目前没有人知道。

如果把用二进制表示的斐波那契数列前511个元素绘制出来，是这个样子的Wolfram Research）：

是不是有点分形的味道？

第

项：分别是2，21，209，2090，20899，208988，2089877，20898764…。（Sloane’s A068070）也就是说，这一数字不断接近208987640249978733769…的前几项。而208987640249978733769…和这样一个数有关：

Binet公式：这个公式不是轨道力学里的那个常用的同名公式，而是给出斐波那契数列第n项的另一个公式，是Jacques Philippe Marie Binet在1843年发现的：

看到了什么？是不是括号中的两个数似乎和黄金分割有关？

斐波那契数列与黄金分割

苏格兰人Robert Simson证明了，当项数趋于无穷时，斐波那契数列的后项与前项之比趋近黄金分割，也就是1.61803398875…。这也许说明了斐波那契数列与黄金分割有天然的联系。

如斐波那契螺旋就是最直接的例子。如果顺逆时针螺旋的数目是斐波那契数列中相邻的2项，可称其为斐波那契螺旋，也被称作黄金螺旋。这样的螺旋能最佳利用圆周，疏密最为均匀。它的构造方法也不难，只需先用同样是与斐波那契数列有关的数构造黄金矩型（长宽之比为黄金分割），再在每个矩形中各描绘出一条1/4圆弧，让各段弧彼此连接。这样的黄金矩形也往往能一些艺术名作中找到，如达·芬奇著名的作品《蒙娜·丽莎》。

计算机绘制的斐波那契螺旋

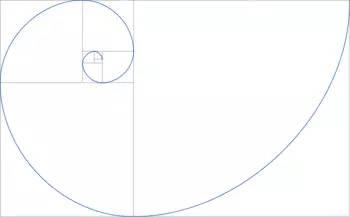
斐波那契螺旋与黄金矩型

自然界中的斐波那契数列

最典型的例子就是以斐波那契螺旋方式排列的花序或树叶。蓟、菊花、向日葵、松果、菠萝……都是按这种方式生长的。如此的原因很简单：这样的布局能使植物的生长疏密得当、最充分地利用阳光和空气，所以很多植物都在亿万年的进化过程中演变成了如今的模样。当然受气候或病虫害的影响，真实的植物往往没有完美的斐波那契螺旋。

每层树枝的数目也往往构成斐波那契数列。

曾在网上看到下面这样一组图，说的是花瓣数符合斐波那契数列各元素的各种植物，也许仅仅是巧合？

另外，晶体的结构也往往与斐波那契数列有关。人们早就发现，在自然界的晶体中，原子以重复的样式排列，不同的化合物也许会出现不同的排列方式，但都是简单的平移重复而已。下面是几张来自晶体中的图案模型。

在图a中，我们可以看到每个原子被其他三个相同的原子包围，形成了一个单位样式，这称为三重对称，因为如果把其中之一沿着平面转过120度，将与另一个发生重叠。而在四重对称（图b）中，转过90度后可得相同图形，在六重对称（图c）中，转过60度可得相同图形。

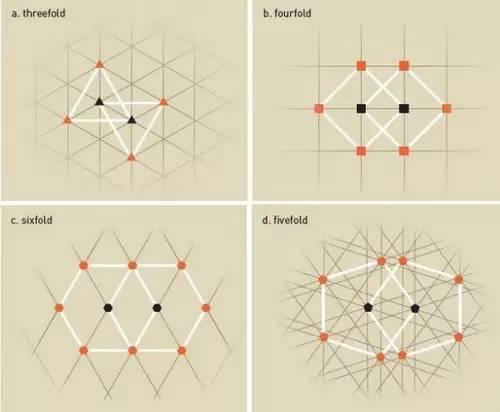
但无论如何，五重对称（图d）却不可能得到，因为其中原子间的距离长短不一，这个样式无法实现旋转对称，由此很容易就充分证明了在晶体中找不到五重对称，依此，七重对称或者更高重的对称都是找不到的。

所以，早期晶体学家们都根深蒂固地认为，五重或七重以上的对称不符合自然规律。

然而，1982年4月的那个早晨，以色列理工学院的Daniel Shechtman却发现在他电子显微镜下面，一个衍射图案可以安然转过圆周的1/10（也就是36度）依旧得到原来样式，也就是说，发现了十重对称！

很快，他又从铝锰合金中找到了五重对称的图案。在那个时期，这项工作绝对是颠覆性的了，以至于相关论文1984年夏天被Journal of Applied Physics断然拒掉。还好，Physical Review Letters没做同样的武断之事，随后就发表了他的文章。Shechtman发现的固体形态被命名为准晶（quasicrystal），以示与传统晶体的区别，并被认为是介于晶体和非晶体之间的一种形态。

Daniel Shechtman获得了2011年的诺贝尔化学奖

著名应用数学家Roger Penrose爵士

事实上，无独有偶，同一时期的数学家们已为他做好了理论铺垫，英国人彭罗斯（Roger Penrose）差不多同一时期便在前人工作基础上提出了一种以两种形状的拼图铺满平面的解决方案。对于Shechtman的准晶体衍射图案和彭罗斯的镶嵌瓷砖来说，都有一个迷人的性质，就是在它们的形态中隐藏着美妙的数学常数τ，亦即黄金分割数1.618……。

彭罗斯瓷砖以一胖一瘦两种菱形（内角分别为72度、108度和36度、144度）镶拼而成，两种菱形的数量之比正好是τ；同样的，在准晶中，原子之间的距离之比也往往趋近于这个值。

往期内容回顾：

内裤简史

一名代孕者的自白

他是个孩子，但也是一个杀人犯！

译言给你的礼物

斐波拉契从一对兔子的繁殖开始，推论出了“兔子数列”亦即斐波拉契数列。由此递推数列，我们可以发现养一对兔子，一年之后就会发展壮大成一个养兔场。人们从斐波拉契数列出发得到了很多有益的和有趣的结果。比如斐波拉契数列与黄金分割（0.618）的关系，并且直到现在还在优选法和运输调度理论中起着基本原理的作用；又如种向日葵的农场主在葵花籽的分布规律上发现了斐波拉契数列，乃至好多植物的花瓣叶序上发现的斐波拉契数列奇观形成了至今未解的“叶序之迷”。可见一个“养兔问题”竟揭示了大自然的一个普遍存在的奥秘。想要了解斐波拉契与兔子繁殖这一数学问题的历史，欢迎阅读《斐波那契的兔子：现代数学之父与算术革命》探寻斐波拉契其人及“兔子数列”的奥秘。