就从例子入手吧。

“不用任何公开参考资料，估算今年新生儿的出生数量？”

“估算你所在的城市，每年收集到的家庭垃圾的总重量是多少？”

“估算此时此刻的世界上，有多少人正在挖鼻孔？

普通人遇到这种问题会懵了，这让我怎么分析？这个问题的意义在哪？

这类问题并不是要看到一个具体的答案，而是需要看到整个分析问题的过程。

下面我来教教你们，希望对你们有启发。

其实这样的题目看似无法回答，但实际上主考官考验的是你的数据思维能力，如何在数据不明确、以及各种限制条件下，利用一些假设的理由和经验推算出正确答案。

这也就涉及到了我们今天要分享的数据分析思想——费米问题。

一、神奇的费米问题

费米是意大利裔的美国物理学家，曾在1938年获得诺贝尔物理学奖，而他被世人所更为熟知的，则是他在芝加哥大学课堂上凭空抛出的一个看似荒谬的问题：

“芝加哥有多少个钢琴调音师？”

听到这个问题的学生都是一脸茫然，费米则提示遇到这样看似庞大的问题，可以把这个问题分解成一些便于操作和认知的小问题，根据猜测和假设去估算问题。

这也就是费米问题思想的核心：逻辑拆解。

也就是说把一个庞大的、抽象的、复杂的问题，逐级拆解为微小的、具体的、简单的问题，然后再将这些小问题进一步拆解，只要保证了逻辑关系，那么将这些可以回答的小问题答案，逐步反推到费米问题上，就可以得到最终的准确答案。

在麦肯锡分析思维中，这种方法叫做“逻辑树法”。

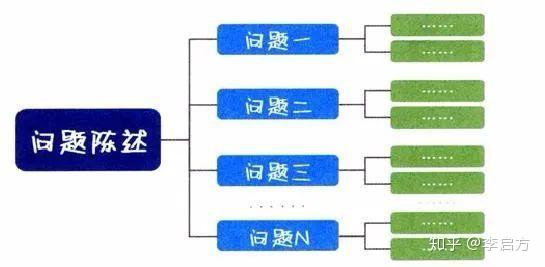
现在我们再回过头来，看一下费米是怎么解答的呢？

首先费米将这个问题拆解成了两个问题：每年芝加哥全部调音师的工作时长，以及一位调音师每年的工作时间。

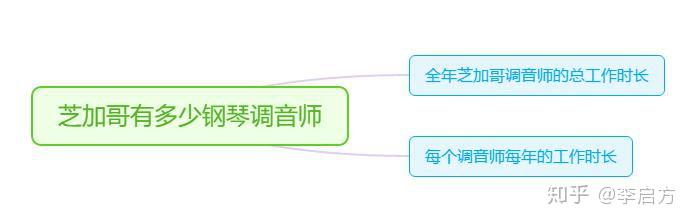
为什么要拆解成这两个问题呢？因为我们在拆解问题的时候需要按照一定的逻辑关系，这个逻辑关系必须要保证能够完全覆盖费米问题的所有范围。

比如这个问题的拆解逻辑是：

总人数=总时长/单个时长

然后我们再先看一下，每年芝加哥全部调音师的工作时长是多少？费米继续将这个问题进行拆解，拆解为了3个问题：

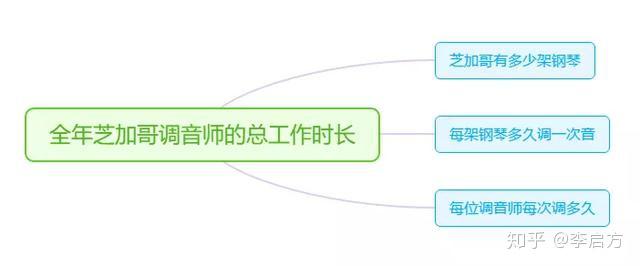
拆解逻辑是：

钢琴数*每年调音次数*调音时长=每年总调音时长

现在问题又变成了芝加哥有多少钢琴和每年调音的次数，这样的问题还能继续拆解吗？

答案是不能，这样的问题就属于费米问题的基本问题，基本问题的确定就要涉及费米问题的另一个主要思想：问题估算。

二、天才的大数估算法

对于基本问题的估算方法，费米给出了一个天才式的估算方法：

对于小问题的估算，不要估算其本身，而是先估算其上下界，然后在10倍的范围内估算出数值，这种方法竟然能保证极高的准确率。

至于原因，我们稍后再讲，先看一下费米是怎么估算的。

首先是如何知道芝加哥的钢琴数，费米先估算了芝加哥总居民数是300万（这个不用估算也基本能知道），平均每个家庭有4个人（美国四人家庭居多），那么芝加哥估计会有75万个家庭。

这些家庭中有多少有钢琴呢？在当时的美国，钢琴属于半稀缺物品，拥有钢琴的家庭应该不会超过1/2，也不会低于1/10，因此费米估算为1/3，那么全市大概会有25万架钢琴。

第二个基本问题是每架钢琴每年需要调音几次，调音师不是常见的岗位，调音次数应该不会超过1年3次，也不会低于10年1次，因此费米估算为3年1次，也就是每年0.33次，那么每年全市有8.3万架钢琴需要调音。

第三个基本问题是调音一次要花多久，不会超过10小时，也不会低于1小时，因此费米估算为3小时。

这样第一个大问题我们就解决了，总钢琴的总调音时长大约是3*83000=249000

下面估算第二个大问题：每年每位调音师工作多久？

假设调音师一年工作250天，算上他每天需要往返的路时，那么他一年的工作时间就是250*24*0.6=3600H

这样所有的问题都已经估算出了结果，最终调音师数量=249000/3600=69位

那么实际上有多少人呢？经过费米和学生们事后进行电话号码验证，大概芝加哥市有80位调音师，除去一些号码重复的，其结果竟然跟费米估算的相差无几！

三、暗中帮助的平均律

但是可能有人会产生质疑，如果将费米估算中家庭拥有钢琴率改为1/5，而不是1/3，其结果不就会改变了吗？费米的这些估算难道都是巧合吗？

其实，费米估算法中涉及到了一个数据概念：平均律。

他的原理是在任何一组计算中，估算带来的错误都可以相互抵消，所做的假设越多，被抵消的概率就会越大。

也就是说，有人会假设1/5的家庭拥有钢琴，他也可能同时会假设每架钢琴需要1年调1次音，而不是3年调一次，这样一高一低，错误估计就会被相互抵消。

换成数据分析的语言就是，你在假设或者猜测某一个小事件的时候，你的推测假设有可能有的过高，有可能有的过低，如果这些“点”的数量足够，最终误差就会被相互抵消，整体结果最终会呈现为一个平均值，这就是平均律理论。

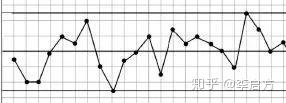
其实就类似于上图，我们确定一个估算上边界，以及一个估算下边界，所有落在这个范围里面的点都会趋向于平均值，落在平均值上的点和平均值下的点就会相互抵消消除，其结果也就趋于一个准确值了。

这也就是为什么费米估算法会百试百灵，准确率十分之高了！

四、费米思想如何用在数据分析中

费米估算法求出的是一种数量级上的准确，这种准确是由一些要素保证的，首先是模型的准确性，这是基础，无论是物理定律还是生活经验都要经受住检验；

其次是变量估计的准确，这个很好理解，你对这个变量越不确定，答案就有可能越不靠谱；

第三条很重要，是对第二条的补救，对一个变量组，每个变量都选择可能性最大的值，最后会在概率意义上得到很好的结果（通俗地说，有可能估计大也可能估计小了，但是最后抵消了，所以参数越多，稳定性越好）。

所以说，费米处理问题的方式是将复杂、困难的问题分解成小的、可以解决的部分，从而以最直接的方法迅速解决问题。这种思维方式非常实用，可以帮助我们解决很多日常甚至重要的问题。

在实际生活中，我们常常需要在信息不全的情况下做出判断决策，要使我们的决定尽可能正确，最有效的策略就是“费米思维”。

我是做数据分析的老李 @李启方，有任问题都可以与我交流。