微积分内容可以分为三部分:微分学、积分学和微积分的应用。
微分学主要讨论两个无穷小之比 \frac{0}{0} ,比如瞬时速度的定义、曲线切线斜率的计算问题等
积分学主要讨论无穷多个无穷小之和\sum_{n=1}^{\infty}0,比如曲边梯形面积的计算、物体重心、引力等
大学微积分课程的教学顺序通常是先讲微分学和积分学内容,然后再讲相应的应用。比如,讲完导数之后,利用导数的几何意义,就可以计算曲线的切线斜率;讲完定积分定义之后,利用定积分的几何意义,就可以计算曲边梯形面积的面积。
但是,微积分产生的历史背景并不是按照先有完整的微分学和积分学理论,然后再利用微分学和积分学理论去解决实际的应用问题,而是先出现了很多的实际应用问题,然后再慢慢地建立和完善微分学和积分学理论。下面简要介绍一下微积分产生的历史背景。
微积分产生的历史背景:
到了十七世纪,有许多科学问题需要解决,主要有四大类:运动中速度与距离的互求问题、曲线的切线问题、最值问题和求和问题,下面我举两个大家比较容易理解的例子:
例1:对于匀速运动,可以知道物体在任意时刻的速度,等于物体经过一段时间的位移与时间之比,即
v(t)=\frac{s(t+\Delta t)-s(t)}{\Delta t}
但是对于变速运动,要计算某一时刻的瞬时速度,就没有办法照搬匀速运动的速度计算公式,同时,对于瞬时速度的定义当时都没有办法使用数学公式表示出来。
例2:对于曲边围成图形的面积的求解。早在公元前,古希腊人已经能够将多边形的面积可以分解为三角形的面积之和来计 算任意多边形的面积。但是对于曲边围成图形的面积难以求解。阿基米德发展“穷竭法”用于求解曲边、曲面面积和旋转体体积等。例如,计算由抛物线 y=x^2 与直线y=0 和 x=1 围成的曲边三角形的面积:
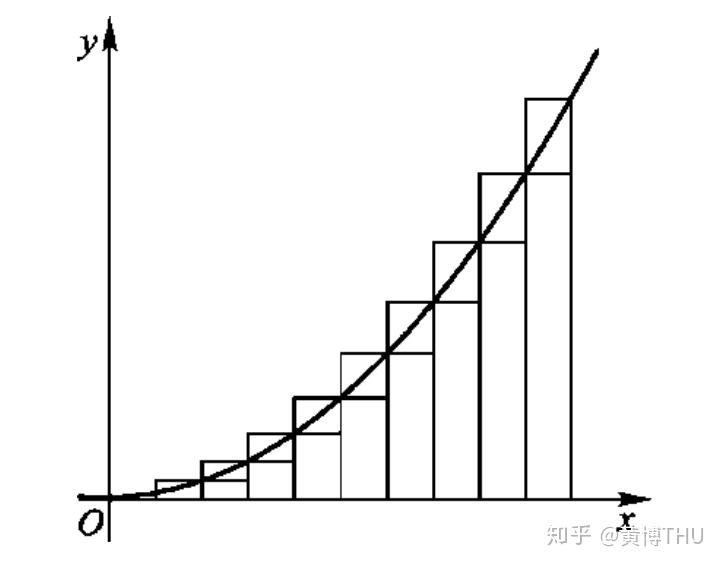
将底边 n 等分,相应的分点是
\frac{0}{n},\frac{1}{n},\frac{2}{n},\cdots,\frac{k}{n},\cdots,\frac{n-1}{n},\frac{n}{n}
从左边数第 k 个大、小矩形的面积分别为:
\frac{1}{n}(\frac{k}{n})^2,\quad \frac{1}{n}(\frac{k-1}{n})^2
大、小矩形的面积和 S_n 、 s_n 分别为:
\begin{equation*} \begin{aligned} S_n = &\frac{1}{n}\cdot\frac{1}{n^2}(1^2+2^2+\cdots+n^2)\\ =&\frac{n(n+1)(n+2)}{6n^3}=\frac{1}{3}+\frac{1}{2n}+\frac{1}{6n^2}\\ s_n = &\frac{1}{n}\cdot\frac{1}{n^2}(0^2+1^2+\cdots+(n-1)^2)\\ =&\frac{(n-1)n(2n-1)}{6n^3}=\frac{1}{3}-\frac{1}{2n}+\frac{1}{6n^2}\\ \end{aligned} \end{equation*}
当 n 越来越大的时候, S_n 和 s_n 都会越来越接近 1/3 ,而曲边三角形的面积介于S_n 和 s_n之间,因此,阿基米德认为抛物线下的面积就是 1/3 。
“穷竭法”已经具有“无限细分”和“无限求和”的现代微积分思想,但是用穷竭法计算曲边形的面积时,对不同的曲边形,采用不同的直边形去逼近,并且计算的过程中采用了特殊的技巧,因而不具有一般性,无法向一般的曲边形推广。
十七世纪的许多著名的数学家、天文学家、物理学家都为解决上述几类问题作了大量的研究工作,为微积分的创立做出了贡献,比如法国的费尔玛、笛卡尔、罗伯瓦、笛沙格,英国的巴罗、瓦里士,德国的开普勒,意大利的卡瓦列利等。
十七世纪下半叶,在前人工作的基础上,英国大科学牛顿和德国数学家莱布尼茨分别在自己的国度里独自研究和完成了微积分的创立工作。但是牛顿和莱布尼茨创立的微积分基础都是基于无穷小分析,但是他们对于无穷小的定义是模糊不清的,有时候认为无穷小是0,有时候又让无穷小不是0,也被称为“贝克莱悖论”。无穷小量究竟是不是零?无穷小及其分析是否合理?由此而引起了数学界甚至哲学界长达一个半世纪的争论,造成了第二次数学危机。
十八世纪,欧陆数学家们力图以代数化的途径来克服微积分基础的困难,这方面的主要代表人物是达朗贝尔、欧拉、拉格朗日和波尔察诺。法国数学家柯西和德国数学家魏尔斯特拉斯进一步将微积分严格化。
简要总结:
微积分理论的创立和完善是发源于对实际应用的需求,但是微积分不仅仅用于解决实际问题,而是抽象出一套更本质的数学理论。举两个简单的例子:
例1:曲线的切线斜率可以使用导数进行计算,但是反过来函数的导数意义并不是都应用着曲线的切线斜率,比如二阶导数、三阶导数,以及更高阶导数,就很难说它对应着曲线的哪些几何意义;
例2:曲边梯形的面积可以使用定积分进行计算,但是任意一个定积分它并不一定对应着哪个面积。
在学习微积分过程中,应当经常借助几何意义和物理意义来辅助理解微积分的概念、定义和定理,因为很多微积分的概念、定义和定理的发源都是来自于相应的几何意义和物理意义;但是同时也要注意不能过分依赖于几何意义和物理意义,因为也有一些微积分的概念、定义和定理的内容很难找到相应的几何意义和物理意义。
最后,关于微积分的具体学习建议,以及参考书、辅导书推荐,可以参考我的另一篇回答。
