表中最后一栏，备注，讲的是该心的性质，性质的推导很简单，我讲一下需要用什么推。建议同学们在大脑里推导一下，这是几何基本功。

中位线，是个解析几何，平面向量中常用的技巧。

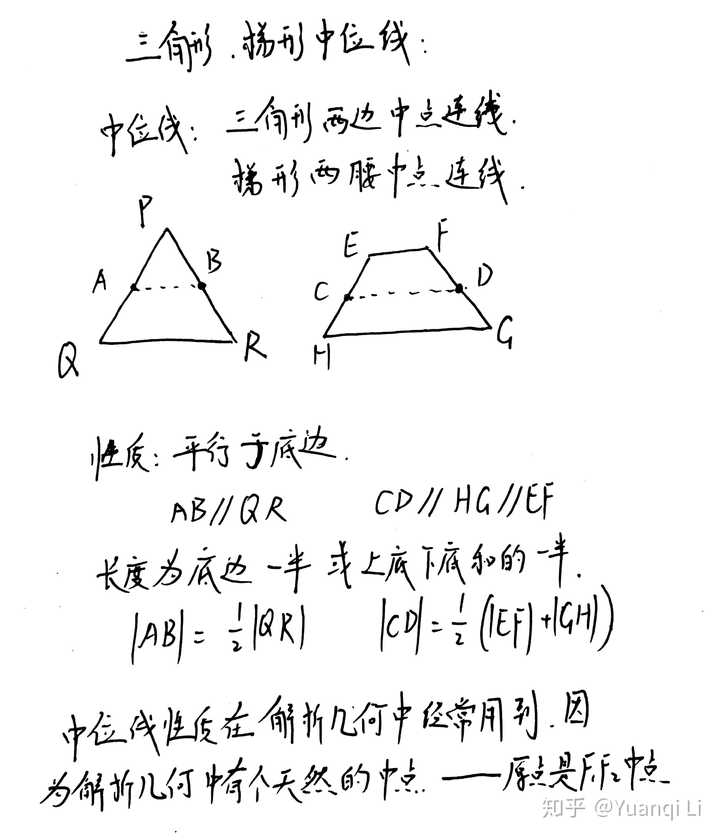
三线合一性：等腰三角形中线，高，角平分线，三条线重合（知道中点可以推垂直，知道垂直可以推中点）

全等三角形，相似三角形。

判定和性质。需要注意：全等三角形，SSA无法判断，因为会出现一个钝角三角形一个锐角三角形的情况。

圆：

垂径定理：有一条弦a，另一条弦b满足以下五个条件中的两个的时候，可以推出另外三个：1，b垂直于a；2，b平分a；3，b平分a所对的优弧；4，b平分a所对的劣弧；5，b过圆心。

平行弦定理：两条平行的弦所夹的弧相等。

弦切角定理：一条切线和过该切点的弦的夹角等于该弦所对的圆周角

圆周角定理：同弧所对的圆周角大小是圆心角的一半。

以上的初中平面几何内容如果你感到陌生，建议学习一下。平时你看到某个学霸学东西比你快，很大程度上其实是因为他的基础比你好。

（三）异面直线的夹角，线面角，二面角

立体几何的大题主流做题流程一般是这样的——第一问用几何方法做，第二问用空间向量。因为第一题如果也用空间向量，时间上可能会亏一两分钟，第二题要用几何方法的话，又增加了答卷的不确定性。当然，这可能只是百分之八十的情况，有时候第一题也是用一下空间向量比较方便的。

在这种主流做题流程下，同学们需要锻炼的，既有第二问要快速，准确地计算空间向量，也有第一问可以稳定快捷地找出几何方法，毕竟，如果你第一问花了三分钟没想出来，又转头去用空间向量，就有点小亏。当然，考场上真遇到这样的状况，也不必慌。

2018年全国2的大题第一问，作为第一个例子，体会一下对题目条件，和对题目要求的双向处理。

第一问，让证明PO垂直于一个平面，那就在平面ABC上找两个垂线。首先已经有一个天然的垂线——AC，三角形PAC根据题目条件是等边三角形，三线合一性：PO既是中线也是高。

再找一个垂线——这里有个思路技巧。证明同面的线段垂直比证明异面线段简单得多，那再找个同面的线段，只能连接BO。其实这里随便找个ABC里面的直线，他都是垂直于PO的，但是BO方便，它就在POB三角形里，三角形的三边直接是可以求出的，显然可以直接用勾股定理证明PO垂直于OB，所以PO垂直于平面ABC。

（四）平行和垂直

选择题，先定性观察一下，垂直基本上是不可能了，就看能不能证明平行或者相交。线面平行，要么在平面上找个线和要证直线平行，要么找到该线所在的平面和要证平面平行。（我们按条件进行总结，还有一种反向的思路，就是按要做的目标进行总结——要达到这个目标，需要什么中间结果）

PN在平面 CNB_1C_1 内，这个平面里两条直线都跟待证平面平行：NB1平行于AM，因为平行四边形，NC平行于MC1，因为直棱柱上下面平行。因此，证明出待证线面平行。

E是中点，这个题又是证明平行的。而证平行，经常是用一串连续平行。那么，我们把三角形一边中点这个条件用成三角形中位线。在设PA中点为F，连接EF，EF//AD//BC，EF=1/2AD=BC，那么EFBC是平行四边形，则CE平行于BF，平行于平面PAB。

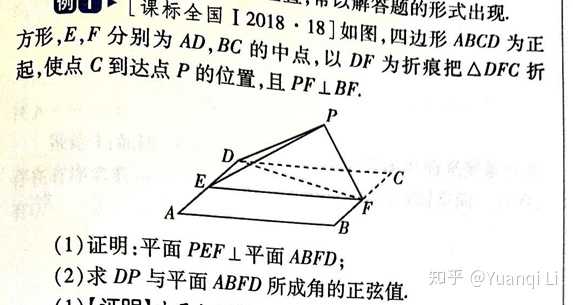
证明平面垂直，先证线面垂直。好找垂直的是BF垂直于PEF。BF垂直于PF和EF，一个是条件，一个是矩形ABFE导出。

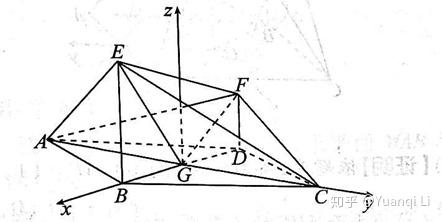
这题稍微有些难。原图一看就发现线太少——因为这样菱形的条件没法用。先把菱形对角线连起来，如图。发现要证垂直，FG和EG最好用。对称可以得到，EA=EC。EG是等腰三角形中线，等腰三角形三线合一性，EG垂直于AC。接下来只需要再证明EG垂直于FG就行。那就需要证明三角形EGF是个直角三角形。我们通过边长符合勾股定理来证。

设BG=1，顶角120度的三角形ABC中， AG=\sqrt{3} ，因为AE垂直于EC，三角形AEC是等腰直角三角形， EG=\sqrt{3} ， BE=\sqrt{2} ，题目条件DF=1/2EB，那么可以在梯形EFDB里，可以解出来 EF=3\sqrt{2}/2 ，三角形FDG里，FG= \sqrt{6}/2 。可得三角形EFG是直角三角形。EG垂直于FG，所以EG垂直于ACF，所以平面垂直。

小结：1，数学的学习方法——按条件做总结，除了总结条件的处理方法，还得总结遇到要证的结论，怎么转化成先证哪个中间结论。2，平面几何是立体几何的基础，中位线，等腰三角形三线合一性等等都必须非常熟悉，才有可能快速做出来题目。

（五）球，棱锥，棱柱等几何体

基本知识就是相关的表面积和体积

求最大值，显然是和函数结合起来考察。既然是和函数结合起来，要求最值的体积是因变量，可调整的因变量是三角形ABC的边长，设为x。

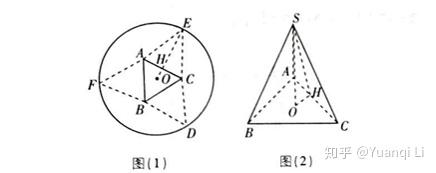
连接OE，等边三角形的知识，可以解出OH，EH，进而勾股定理可以解出来三棱锥的高，三后表示出y关于x的函数，求函数最值。

模块三：平面几何和平面向量

高中数学必考部分并没有讲到平面几何中那些圆，直线，三角形等知识，这些知识都在初中就讲过了。我在前面立体几何章节也做了复习讲解。高中有平面向量章节，高考中会把平面几何和平面向量结合起来考。

圆和直线的方程：二维平面中，如果y和x最高次项都是二次项，而且二次项系数是1，则是圆的方程，若不是1，则是其他圆锥曲线。

题目给出了直线斜率和AB长度，因为梯形ACDB是个直角梯形，所以只要再能知道角DCE，就可以在直角三角形中根据AB长度，也就是CE长度，算出CD。给出了直线方程，斜率是m，所以只要求出m即可。在三角形OAB中求解，OB= \sqrt{12} ，设AB中点是F，三角形ABO是等腰三角形，三线合一性，OF垂直于AB，直角三角形AOB中可以求出来OF，即为原点到直线的距离，代入可以解出来m。

平面向量：

三点共线的证明：

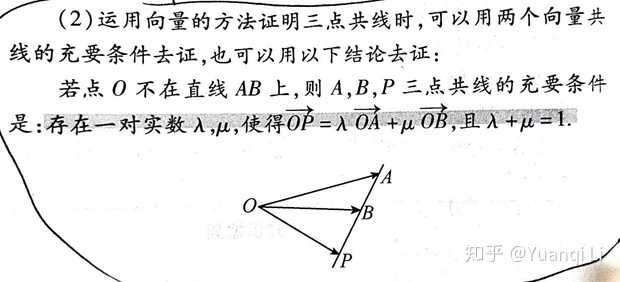
看一个例题：

题目里面有一大堆O，但是问的是三角形ABC。相当于没有O什么事，那么，我们可以把O约掉。这也很容易——用三角形定则即可。我们随便画个图，选个原点，随便画两个点A，B，在三角形ABO中，三角形定则可得：OB-OA=AB，相应的，不等式两侧的向量可以化简为：CA+mBC大于等于BA。然后，用例题附答案的第二行的推导，即可得出结论：无论m去多少，也就是无论D在直线BC上怎么运动，AD长度都大于等于AB长度，则B为垂足。

未完待续，我想在这里逐渐更完高中数学所有模块，敬请期待

——————————————

最后我说一下数学考试的心态调节问题——因为这事关高考成败——可能在高考引发连锁反应最后雪崩。因为高考数学的时间点，实在是个最危险的危机爆发点。

数学第一天下午考，你可能第一道大题就被卡住，你可能遇到了从未见过的考点，你可能会觉得题目很难，也可能觉得很简单，也可能觉得很怪异，这都没关系，考完回来，安心吃饭睡觉，千万不要问别人对数学卷子难度的估计。即便第一道大题就不会做，也不要影响当天晚上的心情，一道数学大题也就十二分，仅仅相当于两个理综选择，所以，决战在第二天，切忌因为数学的损失而影响当天晚上的心情以及第二天的状态。有很多同学，考完数学觉得自己一道前面的大题没做出来，心情特别差，家长也着急，结果第一天晚上的家里或者宾馆就成了修罗场，影响了第二天的理综，数学一道大题也就12分，考理综的时候心态崩了，可能三四十分就没了。

这里我强调的考场心态调节是个技术问题，不是鸡汤，非常重要！（到了高考当天，什么鸡汤都不管用）

找对方法，踏实积累，看到自己的积累日益深厚，成绩自然会提高，分数是知识的自然结果。

未完待续，欢迎关注。我们是树成林，一个有温度的团队，我们的公众号树成林中，每周都会有高考干货分享~我们相信，在我们和你们的共同努力下，树终会成林~

觉得不错的话，点个赞吧，多谢啦！